Veröffentlicht am 21. Juli 2025

Die verschiedenen Höhensysteme – Übersicht und Theorie

In der Geodäsie wird der senkrechte Abstand eines Punktes von einer Bezugsfläche als Höhe bezeichnet. Je nach gewählter Bezugsfläche und Einbezug des Schwerepotentials in die Berechnung gibt es ganz unterschiedliche Höhensysteme. Nachfolgend ein kurzer, zum Teil mathematischer Überblick.

© swisstopo

In der Geodäsie unterscheidet man hauptsächlich zwei Kategorien von Höhen: geometrische und physikalische Höhen.

Geometrische Höhen

Geometrische Höhen, namentlich die ellipsoidischen Höhen, können direkt mit globalen Satellitenmessverfahren wie GNSS (Globale Satelliten Navigationssysteme) gemessen werden. Ihr Hauptnachteil besteht jedoch darin, dass sie nur geometrisch definiert sind. Dadurch kann die Fliessrichtung von Wasser nicht abgebildet werden.

Physikalische Höhen

Physikalische Höhen berücksichtigen die Erdanziehungskraft und zielen darauf ab, die Höhe von Punkten so zu definieren, dass kein Wasser zwischen zwei Punkten fliessen kann, die sich auf derselben Höhe befinden. Je nach Art der Vermessung (Nivellement, GPS) und Bezugsfläche unterscheidet man die physikalische Höhe in

• Gebrauchshöhen
• dynamische Höhen
• Orthometrische Höhen
• Normalhöhen

Diese verschiedenen Systeme haben jeweils theoretische und praktische Vor- und Nachteile, basieren jedoch alle auf der geopotentiellen Kote.

Die geopotenzielle Kote

Die geopotenzielle Kote C eines Punktes P mit der Koordinate x_P ist definiert als die Differenz zwischen dem Gravitationspotenzial auf der Referenzfläche (dem Geoid), W₀, und dem Potenzial W am Punkt P.

C(x_P) = W₀ – W(x_P)

Sie wird in m²/s² angegeben. Eine geopotenzielle Kote kann beispielsweise durch geometrisches Nivellement in Kombination mit gravimetrischen Messungen ermittelt werden. Dazu werden die Höhenunterschiede (in Meter) mit den lokalen Werten der Schwerebeschleunigung (in m/s²) multipliziert.

Um eine Höhe H zu erhalten, muss die geopotentielle Kote durch eine Beschleunigung G₀ geteilt werden.

H(x_P) = C(x_P) / G₀

Je nachdem wie G₀ berechnet wird, ergeben sich verschiedene Höhenarten, die nachfolgend beschrieben werden.

Gebrauchshöhen

Eine Methode, um physikalische Höhen zu bestimmen, besteht darin, ein geometrisches Nivellement durchzuführen. Eines der Hauptprobleme dieser sogenannten «Gebrauchshöhen» ist jedoch, dass sie nicht eindeutig sind. Die Höhe eines Punktes hängt davon ab, über welchen Weg er nivelliert wurde. Folglich kann die Höhe auch nicht von der geopotentiellen Kote abgeleitet werden. Das bedeutet, dass selbst ohne Messunsicherheiten ein und demselben Punkt je nach Messstrecke unterschiedliche Höhen zugewiesen werden könnten.

Zwischen 1860 und 1890 wurde das erste Präzisionsnivellement der Schweiz durchgeführt. Auf diesen gemessenen Punkten – somit auf Gebrauchshöhen – basiert das zurzeit gültige Höhensystem der Schweiz LN02 (Landesvermessung 1902). Als Ausgangspunkt der Höhenbestimmung dient den Findling «Pierre de Niton» im Genfer Seebecken.

Die dynamische Höhe

Wird für G₀ eine Konstante γ₀ gewählt (üblicherweise 9.806 m/s²) ergeben sich dynamische Höhen:

H^dyn(x_P) = C(x_P) / γ₀

Nur die dynamische Höhe ermöglicht einen exakten Zugang zur Gravitationsenergie. Doch selbst bei kurzen Strecken sind die Unterschiede zwischen der dynamischen Höhe und den durch geometrisches Nivellement erhaltenen Höhen erheblich. Um dynamische Höhen zu erhalten, müsste man daher systematisch die geopotentielle Kote heranziehen. Aus diesem Grund werden eher orthometrische oder Normalhöhen verwendet. Diese stellen einen Kompromiss dar, bei dem die Übereinstimmung zwischen der Äquipotentialfläche und den Punkten gleicher Höhe zugunsten einer guten Übereinstimmung zwischen nivellierten Höhenunterschieden und tatsächlichen Höhenunterschieden vernachlässigt wird.

Die orthometrische Höhe

Wird für G0 die durchschnittliche Schwerebeschleunigung entlang der Lotlinie g̅ eingesetzt, ergeben sich othometrische Höhen:

H(x_P) = C(x_P) / g̅

Diese mittlere Schwerebeschleunigung kann jedoch nicht direkt durch Messung ermittelt werden, da es unmöglich ist, ins Innere der Erde vorzudringen. Daher muss auf Massenmodelle der Erde zurückgegriffen werden. Diese enthalten Annahmen über die Dichte der Gesteine zwischen Topografie und Geoid und stützen sich auf gravimetrische Messungen an der Oberfläche.

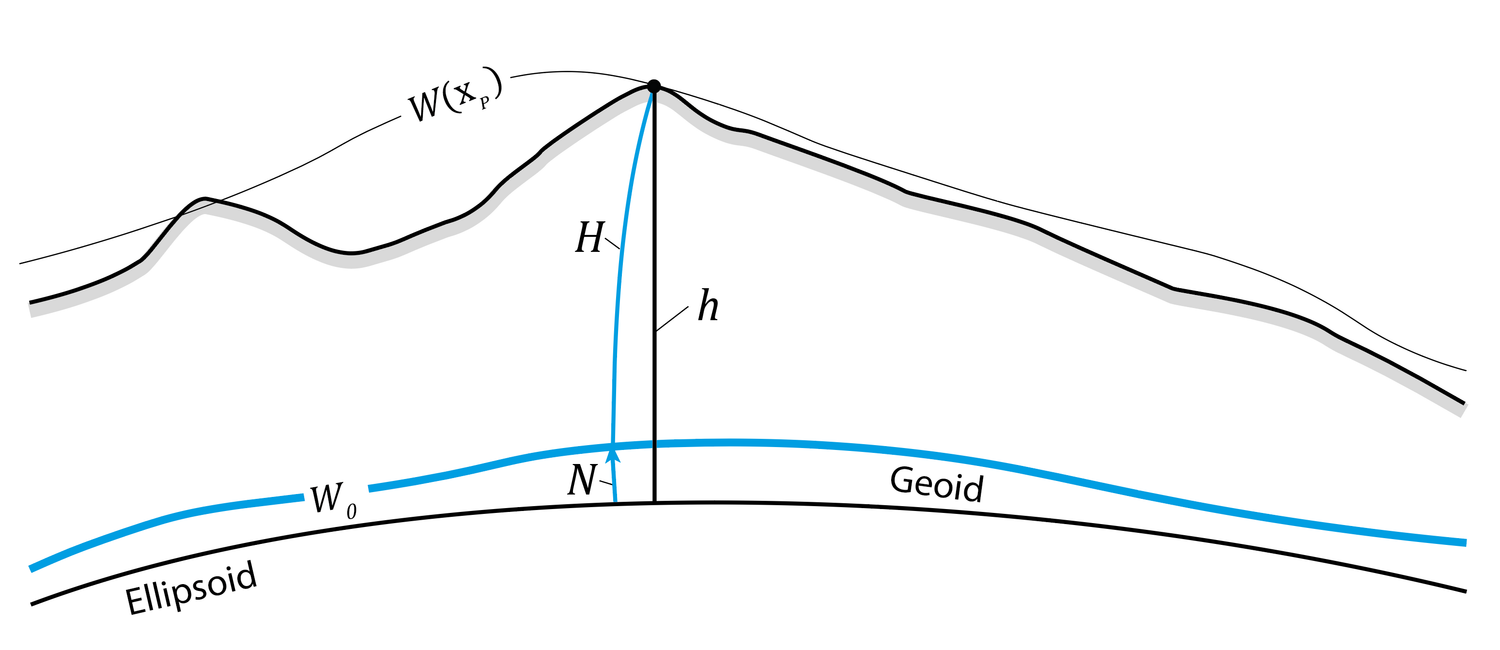
Die orthometrische Höhe ist eindeutig und bezieht sich auf das Geoid. Dabei handelt es sich um eine Äquipotentialfläche, die der unter den Kontinenten verlängerten Meeresoberfläche entspricht. Die orthometrische Höhe H entspricht geometrisch der Länge der (gekrümmten) Senkrechten zwischen dem betrachteten Punkt und dem Geoid. Über die Geoidundulation N ist sie mit der ellipsoidischen Höhe h verbunden:

H = h – N

Normalhöhen

Wird für G₀ die durchschnittliche Normalschwerebeschleunigung entlang der Lotlinie g̅_n eingesetzt, ergeben sich Normalhöhen:

H*(x_P) = C(x_P) / g̅_n

Die Hauptschwierigkeit bei der Bestimmung der orthometrischen Höhe besteht in der genauen Schätzung der mittleren Schwerebeschleunigung g̅. Um diese Einschränkung zu umgehen, schlug der Geodät Mikhail Molodenski in den 1960er Jahren ein alternatives System eindeutiger physikalischer Höhen vor, das ebenfalls auf geopotentiellen Koten basiert. Darin wird die mittlere Schwerebeschleunigung g̅ durch die mittlere Normalschwerebeschleunigung g̅_n  ersetzt, die von einem theoretischen Schwerefeld abgeleitet ist, das von einem homogenen Rotationsellipsoid erzeugt wird, das die gleiche Masse aufweist wie die Erde. (Vgl. Normalhöhen für das neue Schweizer Höhensystem]

Der Vorteil besteht darin, dass sich die mittlere Normalschwerebeschleunigung g̅_n  der Erde ohne Unsicherheiten oder Annahmen über die Massenverteilung in der Erdkruste ermitteln lässt.

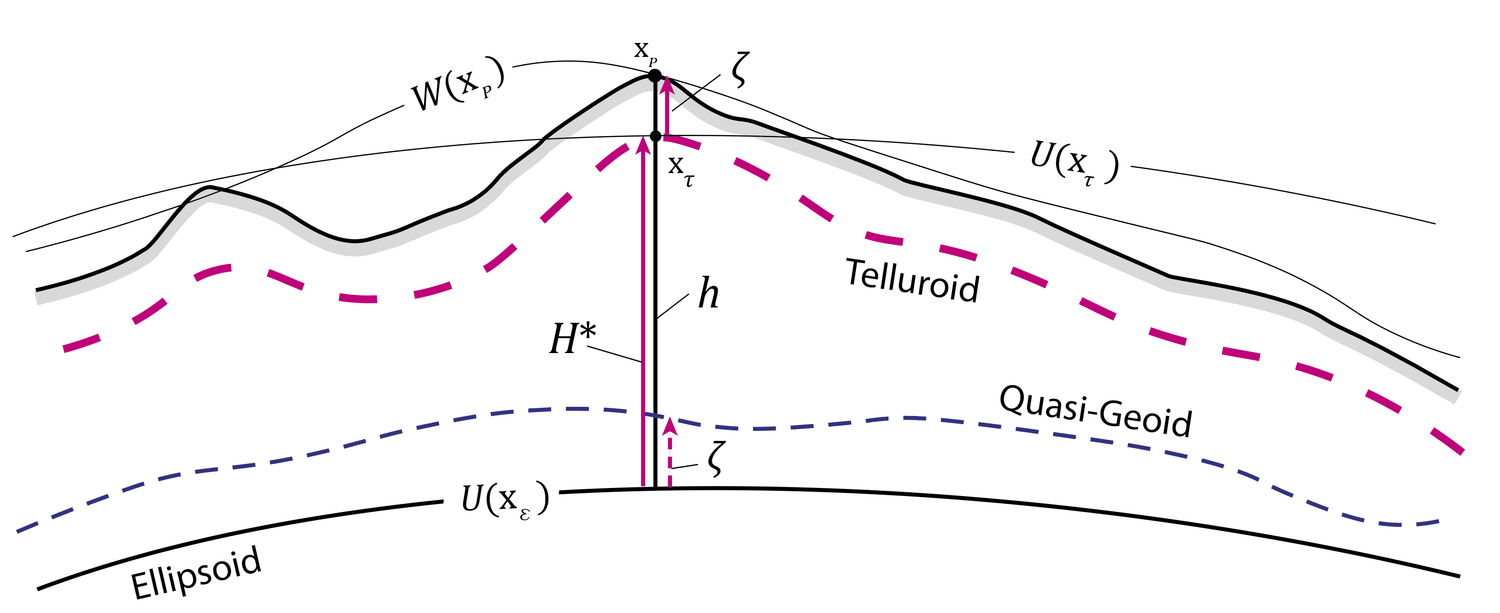
Im Gegensatz zur orthometrischen Höhe bezieht sich die Normalhöhe nicht auf das Geoid oder eine andere Äquipotentialfläche. Ihre Referenzfläche wird als Quasi-Geoid bezeichnet. Um aus einer mit GNSS gemessenen ellipsoidischen Höhe h schliesslich eine Normalhöhe zu erhalten, wird eine ähnliche Beziehung wie bei den orthometrischen Höhen angewendet. Anstelle der Geoidundulation 𝑁 wird jedoch die Höhenanomalie 𝜁 subtrahiert.

H* = h – 𝜁