Publié le 13 août 2025

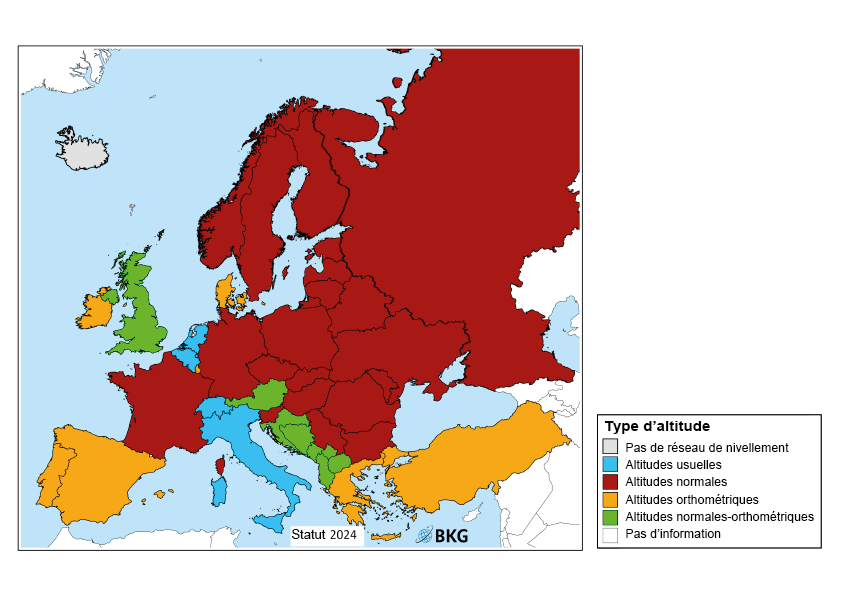
Des altitudes normales pour le système altimétrique suisse

L'altitude normale d'un point situé à la surface du terrain est définie comme sa distance verticale par rapport au quasi-géoïde. Le quasi-géoïde est la surface de référence théorique pour ce type d'altitude. Le nouveau système altimétrique suisse en projet, CHVRS, est basé sur des altitudes normales.

© Bundesamt für Kartografie und Geodäsie, Allemagne

Le choix d'adopter les altitudes normales pour le nouveau système altimétrique suisse CHVRS, bien que conceptuellement plus complexes, repose principalement sur ces deux raisons :

• Elles peuvent être déduites des cotes géopotentielles sans nécessiter d'hypothèses sur la densité des masses.
• Elles sont directement compatibles avec les standards internationaux, notamment ceux adoptés par de nombreux pays européens voisins comme la France et l'Allemagne.

Altitude normale telle que définie par l'approche de Molodensky

Approfondissons un peu la notion d’altitude normale telle que définie par l’approche de Molodensky (géodésien russe, 1909–1991). Cette méthode repose sur une distinction fondamentale entre deux types de potentiels :

• le potentiel de pesanteur W, généré par la répartition réelle des masses à l’intérieur de la Terre,
• le potentiel normal U, généré par un ellipsoïde de référence, choisi pour modéliser de manière simplifiée le potentiel de pesanteur la Terre. L’ellipsoïde est choisi de telle sorte que le potentiel normal U en un point x_ɛ sur sa surface soit égal au potentiel de référence :

U(x_ɛ) = W₀  

L’idée-clé de Molodensky est de s’appuyer sur le potentiel normal U pour définir une altitude. Ainsi, en prenant la défnition de la cote géopotentielle [C(x_P) = W₀ – W(x_P)], et en introduisant la relation donnée par l’équation ci-dessus on obtient :

C(x_P) = W₀ – W(x_P) = U(x_ɛ) – W(x_P)

Ensuite, afin de ne faire apparaître que le potentiel normal U dans l’équation précédente, on définit un point fictif x_𝜏, le long de la ligne d’aplomb, tel que le potentiel normal U(x_𝜏) de ce point fictif soit égal au potentiel réel W(x_P). Ainsi, on peut écrire :

C(x_P) = U(x_ɛ) – U(x_𝜏)

Sans développer ici les étapes intermédiaires, cette différence de potentiel normal peut être exprimée en fonction de la gravité normale moyenne γ̅ et de la hauteur ellipsoïdale du point x_𝜏 :

C(x_P) = γ̅  · h(x_𝜏)

Nous définissions ainsi l’altitude normale comme étant égale à l’altitude ellipsoïdale du point x_𝜏 , c’est-à-dire :

H*(x_P) = h(x_𝜏)

Finalement, en combinant les deux dernières équations, on obtient :

H*(x_P) = C(x_P) / γ̅  

Si l’on détermine le point x_𝜏 pour chaque point de la topographie, la surface obtenue s’appelle le telluroïde (figure ci-dessous). L’anomalie de hauteur correspond alors à la distance (le long de la normale à l’ellipsoïde) entre la surface du telluroïde et la topographie. En reportant ces anomalies de hauteur au niveau de l’ellipsoïde, nous obtenons le quasi-géoïde, une surface théorique jouant le même rôle pour les altitudes normales que le géoïde pour les altitudes orthométriques.