Publié le 14 août 2025

Les différents systèmes altimétriques – aperçu et quelques notions théoriques

En géodésie, la distance verticale entre un point et une surface de référence est appelée altitude. Il existe différents systèmes altimétrique en fonction de la surface de référence choisie et de la prise en compte du potentiel gravitationnel dans le calcul. Voici un bref aperçu, en partie mathématique.

© swisstopo

En géodésie, on distingue principalement deux grandes catégories d’altitudes : les altitudes géométriques et physiques.

Altitudes géométriques

Les altitudes géométriques, exprimées sous forme de hauteurs ellipsoïdales, sont directement mesurables par des méthodes de positionnement satellitaire globales telles que le GNSS. Leur principal inconvénient est qu’elles ne permettent pas d’accéder facilement aux niveaux d’énergie potentielle de gravité (les surfaces équipotentielles), pourtant essentiels dans les applications pratiques. Par exemple, de l’eau peut s’écouler entre deux points situés à la même altitude ellipsoïdale.

Altitudes physiques

Les altitudes physiques tiennent compte de la pesanteur terrestre et visent à définir l’altitude de points de manière à ce que l’eau ne puisse pas s’écouler entre deux points situés à la même altitude. Selon le type de mesure (nivellement, GPS) et la surface de référence, on distingue l'altitude physique en

• Altitudes usuelles
• Altitudes dynamiques
• Altitudes orthométriques
• Altitudes normales

Ces différents systèmes présentent chacun des avantages et des inconvénients — tant théoriques que pratiques — mais ont en commun d’être basés sur la cote géopotentielle.

La cote géopotentielle

La cote géopotentielle C d’un point P à la position x_P est définie comme la différence entre le potentiel de pesanteur au niveau de référence (le géoïde), noté W₀, , et le potentiel W au point P.

C(x_P) = W₀ – W(x_P)

Elle s’exprimée en m²/s². Une cote géopotentielle peut s’obtenir par exemple par des mesures de nivellement géométrique combinées à des données gravimétriques, en multipliant les dénivelées (exprimée en mètres) par les valeurs locales de l’accélération de la pesanteur (en m/s²).

Pour obtenir une altitude H, il suffit de diviser la cote géopotentielle par l’accélération de pesanteur G_0.

H(x_P) = C(x_P) / G₀

Selon la manière dont G₀ est calculé, on obtient différents types d'altitudes qui sont présentés ci-dessous.

Altitudes usuelles

Une méthode simple pour obtenir des altitudes physiques consiste à effectuer des mesures de nivellement géométrique. Un des problèmes majeurs des altitudes dites « usuelles » est qu’elles ne sont pas univoques : l’altitude d’un point dépend du chemin emprunté pour le niveler. Par conséquent, l’altitude ne peut pas non plus être déduite de la cote géopotentielle. Autrement dit, même sans aucune incertitude de mesure, un même point peut se voir attribuer des altitudes différentes selon le cheminement suivi.

Le premier nivellement de précision de la Suisse a été réalisé entre 1860 et 1890. Le système altimétrique actuellement en vigueur en Suisse, le LN02 (mensuration nationale de 1902), repose sur les points ainsi mesurés, c'est-à-dire sur des altitudes usuelles. Le bloc erratique « Pierre de Niton », situé dans le bassin lacustre genevois, sert de point de référence pour la détermination de l'altitude.

Altitudes dynamiques

Si l'on choisit une constante γ₀ (généralement 9,806 m/s²) pour G₀, on obtient les altitudes dynamiques suivantes :

H^dyn(x_P) = C(x_P) / γ₀

Seules les altitudes dynamiques permettent d’accéder rigoureusement au niveau d’énergie potentielle de gravité. De part cette propriété, nous pourrions penser que les altitudes dynamiques constituent les altitudes idéales. Hélas, en pratique, elles ne sont pas idéales. En effet, les différences entre l’altitude dynamique et les distances verticales mesurées par nivellement géométrique sont significatives même pour de petits cheminements. Il faudrait donc systématiquement passer par la cote géopotentielle pour obtenir l’altitude dynamique. C’est donc pour cette raison pratique que ce sont plutôt les altitudes orthométriques et normales qui sont utilisées. Elles font un léger compromis sur l’égalité entre les surfaces équipotentielles et les surfaces d’égales altitudes au bénéfice de la bonne correspondance entre distances verticales géométrique et différences d’altitudes.

Altitudes orthométriques

Si l'accélération moyenne de la gravité le long de la ligne verticale g̅ est utilisée pour G₀, on obtient les altitudes othométriques suivantes :

H(x_P) = C(x_P) / g̅

Toutefois, cette accélération de pesanteur moyenne ne peut pas être déterminée directement par mesure, car il est impossible d’accéder à l’intérieur de la Terre. Il faut donc recourir à des modèles de masse intégrant des hypothèses sur la densité des roches comprises entre la topographie et le géoïde, en s’appuyant sur des mesures gravimétriques réalisées à la surface.

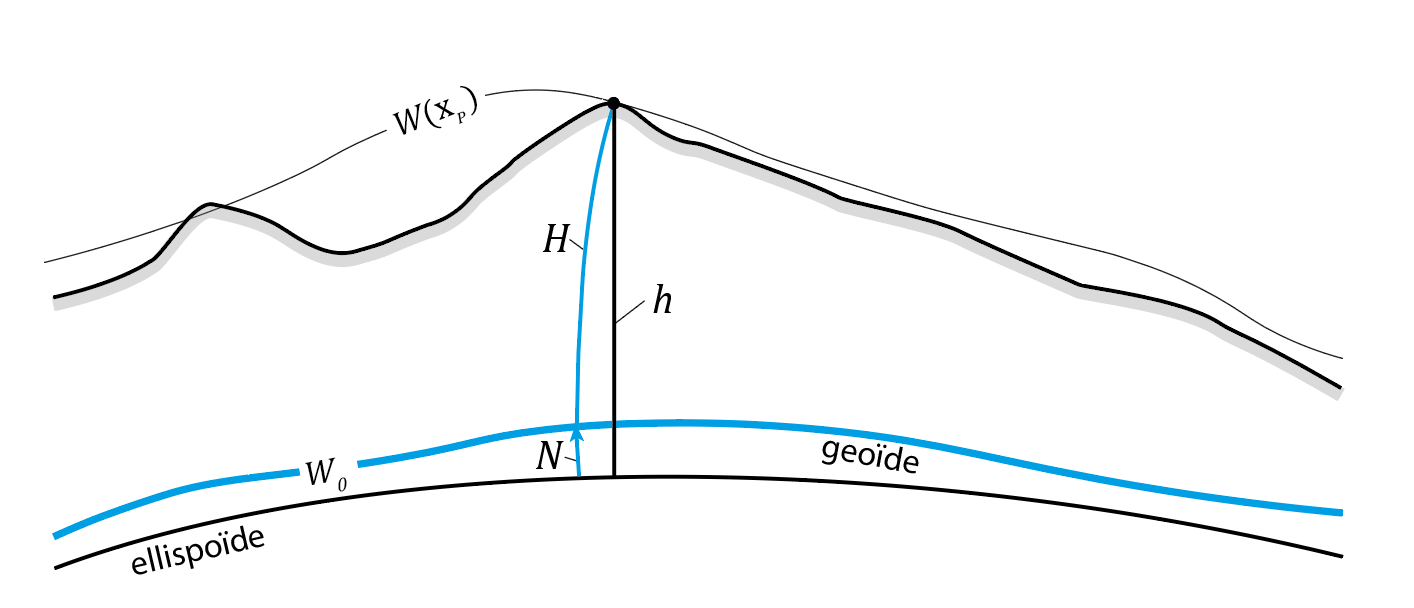
Les altitudes orthométriques sont univoques et se réfèrent au géoïde qui est une surface équipotentielle correspondant à la surface des océans prolongée sous les continents. Géométriquement, l’altitude orthométrique H correspond à la distance curviligne le long de la ligne d’aplomb entre le point considéré et son point correspondant sur la surface du géoïde. Elle est reliée à l’altitude ellipsoïdale h par la cote du géoïde N :

H = h – N

Altitudes normales

Si l'on utilise pour G₀ l'accélération normale moyenne le long de la ligne verticale g̅_n, on obtient les altitudes normales suivantes :

H*(x_P) = C(x_P) / g̅_n

La difficulté principale dans la détermination des altitudes orthométriques réside donc dans l’estimation précise de la pesanteur moyenne g̅. Pour contourner cette limitation, le géodésien Mikhail Molodensky a proposé dans les années 1960 un système alternatif d’altitudes physiques univoques, également fondé sur les cotes géopotentielles. Ce système remplace g̅ par l’accélération de pesanteur normale moyenne g̅_n , calculée à partir d’un champ de pesanteur théorique généré par un ellipsoïde de révolution homogène dont la masse est équivalente à celle de la Terre. (Voir Des altitudes normales pour le système altimétrique suisse)

L’avantage est que l’accélération de pesanteur normale moyenne g̅_n peut être obtenue sans incertitude ni hypothèse sur la distribution des masses dans la croûte terrestre.

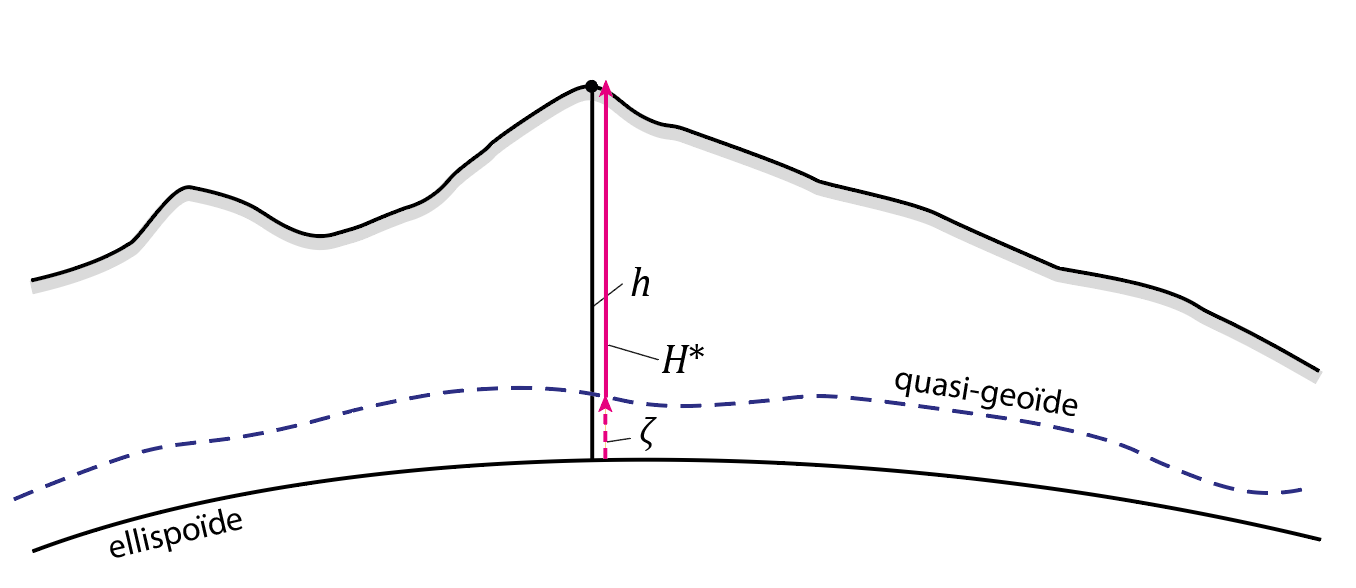
Contrairement aux altitudes orthométriques, les altitudes normales ne se réfèrent pas au géoïde, ni à une autre surface équipotentielle. Leur surface de référence est appelée quasi-géoïde. Enfin, pour obtenir une altitude normale à partir d’une hauteur ellipsoïdale h mesurée par GNSS, on applique une relation analogue à celle utilisée pour les altitudes orthométriques. Cependant, au lieu de la cote du géoïde N, on soustrait l’anomalie de hauteur 𝜁 :

H* = h – 𝜁